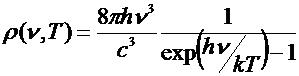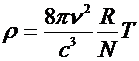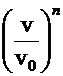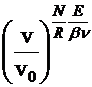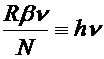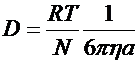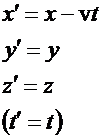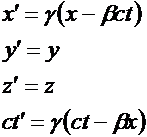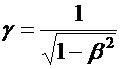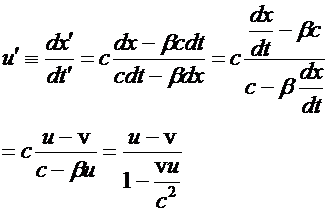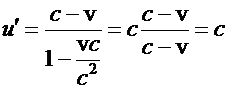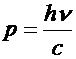Einstein biography, 1879 to 1905
(Click on numbers to see related presentation slides)
Hermann Einstein of
On
Friday, March 14, 1879 their first child was born. The birth certificate reads:
“No.
224,
In
1944, the home on Bahnhofstrasse was bombed. The birth certificate is still in
the
Albert
Einstein had no middle name!!
His
sister, Maria, was born in 1881. Albert called her Maja and was probably closer
to her than to any other human being.
The
family was not religious. Both parents were raised that way. Hermann was proud
of the fact that Jewish rites were not practiced in his home.
Maja’s
biography of Albert in 1924 is the best source about his early years.
He
was born with a big head. I guess head size does matter!! He did not speak for
a long time. Between 2 and 3 he began to speak in whole sentences. He was a
quiet child, preferring to play by himself. He had tantrums and occasionally
threw things at his sister. This ceased at age 7.
Albert
studied violin between 6 and 13, and later learned to improvise on piano. Bach
and Mozart were among his favorite composers.
In
1880 the family moved to
At
5 he received instruction at home. This came to an abrupt end when he had a
tantrum and threw a chair at his teacher (probably frustration at being taught
in a way he did not like). At 6 he entered public school, the Volksschule. “He
was a reliable, persistent and slow-working pupil who solved his mathematical
problems with self-assurance though not without computational errors.” (Maja)
“He did very well.”
In
August 1886, Pauline wrote to her mother: “Yesterday Albert received his
grades, he was again number one. His report card was brilliant.” (Pais p.37)
At
age 4 or 5, Albert was shown a compass by his father. This excited him very
much. In later life, he said of this event: “I had experienced a miracle.”
Uncle Jakob gave him mathematical problems. After he solved them, “the boy
experienced a deep feeling of happiness.” (Maja) At age twelve, he experienced
his second miracle, Euclidean geometry. From 12 to 16 he studied differential
and integral calculus by himself.
Albert
remained quiet and aloof from his classmates. Building a house of cards was a
favorite past-time.
In
1888 he entered the Gymnasium and stayed until age 15. In each year he earned
either the highest or next highest marks in mathematics and in Latin. He
disliked school, authoritarian teachers, servile students, rote learning. He
also disliked sports. He made few friends.
From
10 to 15, Albert was influenced by Max Talmud, a medical student. Every
Thursday he came to dinner at the Einstein’s. He gave Albert popular books on
science and, later, the writings of Kant. The two spent hours
discussing science and philosophy. Albert did not read light literature,
play with boys his age, and his only diversion was music.
Albert
was taught Judaism at home. He went through an intense religious phase when he
was 11 years old. He composed songs in honor of God. This ended a year later
when he was exposed to science. He did not become bar mitzvah. He never
mastered Hebrew.
Hermann
and Jakob’s business slowed and they moved to
Alone in Munich Albert was depressed and
nervous. The prospect of military service worried him. He went to Italy Zurich Zurich
14
On October 29, 1896 he became a student at
the ETH having passed the Matura exam with grades: (6 is max)
German 5
Italian 5
history 6
geography 4
algebra 6
geometry 6
descriptive
geometry 6
physics 6
chemistry 5
natural
history 5
drawing
(art) 4
drawing
(technical) 4
His father’s business failed in 1896, and
again two years later. Not being able to help, troubled Albert. When his father
again got work, the melancholy passed.
15
His friendships with Marcel Grossman and
Michele Besso began in his student days. At the ETH, Albert spent most of his
time in the physical laboratory, “fascinated by direct contact with
observation.” (Pais 44). His professor, Heinrich
Weber, did not encourage him and did not permit him to conduct an experiment on
the earth’s movement against the aether. Albert enjoyed Hermann Minkowski as a
teacher. However, he relied far more on self-study. He studied Lorentz,
Boltzmann and Darwin. Grossman shared his lecture notes with Einstein.
16
His final grades at the ETH were:
theoretical
physics 5
experimental
physics 5
astronomy 5
theory
of functions 5.5
essay
on heat conductivity 4.5
This qualified him as a Fachlehrer
together with three other students in 1900 (he scored fourth out of five
students). The other three became assistants at the ETH but Albert did not and
was jobless. He blamed Weber for not getting an assistantship. One other
student, Mileva Maric, failed the exam. She again failed in 1901. Her glaring
weakness was mathematics. After a year of trying for another position Albert
was still without work.
However, in December, 1900 he finished his
first paper, on intermolecular forces, and published it in Annalen der Physik.
In 1901 he was granted Swiss citizenship.
In 1901 he wrote to Ostwald in Leipzig and to Kamerlingh-Onnes in Leiden Geneva
17
In 1901 Albert finally got a job as a high
school substitute teacher. He wrote:
“After having taught for 5 or 6 hours in
the morning, I am still fresh and work in the afternoon either in the library
on my further education or at home on interesting problems… I have given up the
ambition to get to a university since I saw that also under the present
circumstances I maintain the strength and desire to make scientific efforts.”
18
In September, 1901 he got a job in a
private school in Schaffhausen. He wrote a doctoral dissertation on the kinetic
theory of gases and sent it to the University
of Zurich
Marcel Grossman’s father got Albert a job
as a patent clerk in Bern
Hermann Einstein died in 1902. Albert had
plans to marry Mileva Maric, but was strongly opposed by his mother. Albert and
Mileva had a daughter, Lieserl, in 1902.
19
They married January 6, 1903. In 1904
their son, Hans Albert was born. Hans became a well known hydraulics engineer
at UC Berkeley. A second son, Eduard, was born in 1910. He was a gifted child
but later (1965) died in an asylum for schizophrenics. No one knows what
happened to Lieserl.
Albert did well at the patent office. In
1903 and 1904 he published papers on the foundations of statistical mechanics.
20 21 22 23
“No one before or since has widened the
horizons of physics in so short a time as Einstein did in 1905.” (Pais 47). In that year Einstein produced six papers:
24
1)
The
photoelectric effect and the light quantum, completed March 17. This paper lead
to his Nobel prize and was written before his PhD
thesis.
2)
Doctoral
thesis on a new determination of molecular dimensions and Avogadro’s number,
completed April 30. The published thesis became his most often quoted paper in
the modern literature.
3)
The
Brownian motion paper received by Annalen der Physik on May 11. This was a direct outgrowth
of the thesis and became his second most highly cited paper.
4)
The
first paper on special relativity was received for Annalen der Physik June 30.
5)
The
second paper on special relativity containing E = mc2 was received for
Annalen der Physik September 27. (Actually what is really there is the
statement that a body that emits energy L as radiation has a decrease in mass
of L/V2, where V is the speed of light.)
6)
A
second paper on Brownian motion was received by Annalen der Physik December 19.
25
Little in his earlier published work hints
at this extraordinary creative outburst. Later in life he said that his papers
of 1901 and 1902 were worthless. The next three papers in 1903 and 1904 were of
mixed quality and none left much of a mark on physics.
On July 24, 1905 the faculty of the University of Zurich
At the end of his life, Einstein wrote
that the greatest thing Marcel Grossman did for him was to recommend him to the
patent office with the help of his father.
We now turn to the papers of 1905. The
first one is titled:
26
"On a Heuristic Point of View
Concerning the Generation and Conversion of Light", AdP
17, 132 (1905).
What is it about according to common
usage? The photoelectric effect.
What is it really about? The light quantum hypothesis.
Some history: Gustav Kirchhoff's
pioneering work on black body radiation in 1859 suggested that there existed a
universal function of frequency and temperature for all black bodies. (In
essence a black body is any object that absorbs all radiation incident upon it.)
27
It was this challenge
that eventually lead to Planck's distribution in 1900:
For high frequencies,
i.e.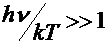 
, Wien's law was known:
28
However, experiments in the classical
regime,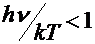 
, were inconsistent with Wien's law: 
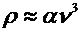and agreed much better
with 
.
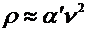Planck's law agreed with both regimes, and
for 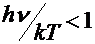gave
Planck used a statistical mechanics
argument in which radiation energy was treated as comprised of packets of
energy in the amount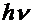 
.
29
Einstein took this idea seriously and
interpreted it to mean that light consisted of quanta with energy .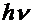
Most of the 1905 paper is about the volume
dependence of the entropy for radiation. For gases and dilute solutions he knew
that the entropy depended on the quantity
for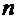 
independent particles
and reference volume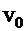 
. For radiation, using the quantum hypothesis, he got
where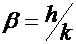 
.
"From this we further conclude that
monochromatic radiation of low density(within the
range of validity of Wien's radiation formula) behaves thermodynamically as if
it consisted of mutually independent energy quanta of magnitude
While this appeared inconsistent with
Maxwell's continuum theory of radiation, Einstein took it seriously, especially
for the interaction of light with matter.
30
Section 7 is about Stokes' rule: 
Section 8 is about the photoelectric
effect: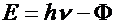 
This implies that if the frequency of
light is high enough for the energy of a quantum, 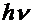, to equal the work function, 
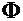, then the energy of emitted electrons is linear in frequency
with a slope given by Planck's constant. This provides a measure of Planck's
constant that is independent of the black body law.
Section 9 is about the UV ionization of
gases
These examples cover only 30% of the
paper.
Robert Millikan's meticulous 1916 studies
clinched the case for most physicists, but not all.
Einstein later said this was the only
truly revolutionary contribution of 1905. Einstein emphasized the
"provisional" nature of the quantum hypothesis and other physicists
were eager to conclude that he had retracted the idea. This was far from the
case.
31
On November 10, 1922 Einstein's residence
received a telegram (he was on his way to Japan) telling him he was awarded the
Nobel prize in physics for 1921. On the same day Niels
Bohr was told he had received it for 1922.
The citation reads:"for his services
to theoretical physics and especially for his discovery of the law of the
photoelectric effect."
"It is a touching twist of history
that the Committee, conservative by inclination, would honor Einstein for the
most revolutionary contribution he ever made to physics." (Pais, p. 511)
32 33
The next topic is Brownian Motion. Einstein’s thesis and two other papers were written
about this topic. The title of the thesis is:
“A New Determination of Molecular
Dimensions”, eventually published in AdP 19, 289 (1906).
Of the other two papers, the main one is
titled:
“On the Motion of Small Particles
Suspended in Liquids at Rest Required by the Molecular Kinetic Theory of Heat”,
AdP 17
549 (1905).
Clearly they are about Brownian Motion according to common usage.
What are they really about? The reality of atoms and molecules and the magnitude of Avogadro’s
number.
For students at the ETH it was possible to
get a Doktor’s degree from the University
of Zurich
During the nineteenth century the reality
of atoms and molecules was still hotly debated. Some chemists took the idea
seriously as did a few physicists who worked on the kinetic theory of gases. Of
course atoms and molecules had to be so small that there was no way to see
them. What their size was and how many were in a mole of matter, Avogardro’s
number, were profound issues at the turn of the century when Einstein began to
think about them.
34
Loschmidt had the idea that one could
determine both size and number from a pair of relations, an idea that Einstein
followed. The two ingredients were: the change in viscosity of a fluid caused
by adding a dilute solute, and a formula for the diffusion constant for the
solute as a function of the fluid properties.
The determination of the former comprised
the bulk of the thesis and used hydrodynamics in a difficult calculation to
give
in which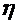 
is the shear viscosity
and the correction factor is the volume fraction of solute molecules.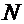 
is
Avogardro’s number and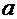 
is the radius of the
solute molecule. Einstein got the coefficient of 5/2 wrong and Burkhardt missed
this error. The second result was Einstein’s real contribution
in which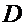 
is the diffusion
constant of the solute, 
is the gas constant
and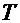 
is the temperature. We have two equations in the two unknowns
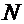and 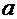. By performing macroscopic measurements of viscosity and by
using a microscope to determine 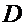, one obtains molecular sizes and Avogadro’s number.
35 36
Brownian motion per se is not
mentioned at all in the thesis. It is only mentioned in passing in the paper
where Einstein writes in the first paragraph:
“It is possible that the motion to be
discussed here are identical with so-called Brownian molecular motion; however,
the data available to me on the latter are so imprecise that I could not form a
judgment on the question.”
Jean Perrin did the first really accurate
measurements in 1909 and received the Nobel prize for
this and related work in 1926. This really clinched the reality of molecules.
37
The third topic is the theory of
relativity. There are two papers from 1905:
“On the Electrodynamics
of Moving Bodies.” AdP 17 891 (1905), and “Does the Inertia of a
Body Depend on its Energy Content?” AdP 18 639 (1905).
Common usage says these papers are about
the special theory of relativity. At the time there was no general or special
theory so these papers were simply about relativity. However, what they are
really about is the invariance of the speed of light, c, and the fallacy of
absolute time.
38
Consider two reference frames labeled by K
and K’, and imagine that K’ moves relative to K with velocity v along a common
x-axis. All physicists use the same values for Planck’s constant h and for the
charge of the electron e in each reference frame, regardless of the relative
motion. This can be phrased by saying that h and e are invariants. Einstein
postulated that the speed of light c should also be an invariant.
39
In Galilean relativity one has
The last equation was for a long time
taken for granted and is the idea of absolute time.
40
This poses a problem. Suppose a body moves
to the right along the x-axis of frame K with velocity u. From the perspective
of frame K’ moving with velocity v relative to K the apparent velocity of the
body is u-v. Indeed, if the frame K’ moves relative to K so that v = u then the
body appears to be at rest in K’.
41
By looking at Galilean invariance in
differential form we see how the velocity difference arises formally.
42
Relative
to K the velocity of light is c. Would it not be c-v
relative to K’? The requirement that it is an invariant means that relative to
K’ it is also c. This requirement forces a connection between the coordinates
and time in K’ and in K given by the Lorentz transformations
in which
and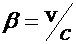 
.
43
These equations are called the Lorentz
transformations. Lorentz published them in 1904, and Poincare published
corrections to the electrodynamics part of Lorentz’ paper in 1905. In Pauli’s
history of the subject he writes:
44
“It was Einstein, finally, who in a way
completed the basic formulation of this new discipline. His paper of 1905 was
submitted at almost the same time as Poincare’s article and had been written
without previous knowledge of Lorentz’ paper of 1904. It includes not only all
the essential results contained in the other two papers, but shows an entirely
novel, and much more profound, understanding of the whole problem.”
45
The Lorentz transformations can be written
for infinitesimal changes in
Now the velocity in K’ is given by
46
47
This is the velocity addition formula with
a correction in the denominator. Remarkably, for 
too!!! c is an invariant !!
48
49
The
invariance theory of Einstein completely changes everything. Space and time are
intimately commingled. The geometry of the world is four
dimensional space-time. The laws of
nature are expressible in terms of Minkowski 4-vectors (and higher order tensor
generalizations) that obey Lorentz invariance.
.